撰写了文章 发布于 2020-03-15 20:24:59
A* 算法实现
A* 算法实现
声明:已联系原作者,取得翻译授权
原文地址:https://www.redblobgames.com/pathfinding/a-star/implementation.html
前文:A*算法介绍(Github地址),【翻译】由浅入深 A* 算法介绍
本文 Github 地址:这里
本文相关代码地址:打开
----------分割线----------
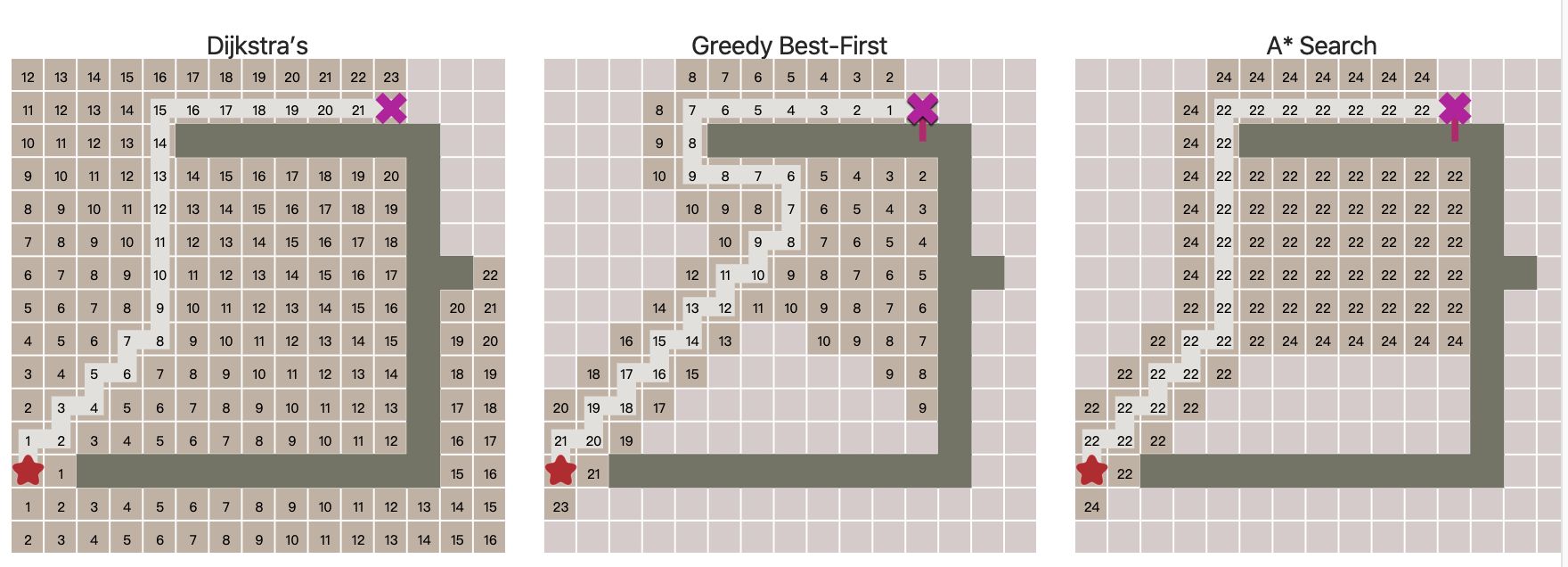
这篇文章是我对A*介绍的配套指南,其中我解释了算法的工作原理。本文我将展示如何实现广度优先搜索、Dijkstra 算法、贪心最佳优先搜索和 A* 算法。我尝试保持代码简洁。
图搜索有一系列相关算法。算法有很多变体,实现上也有很多变体。将本文展示的代码视为一个起点,而不是适用于所有情况的最终版本。
1 Python 实现
我将解释下面的大多数代码。你可以在 Implementation.py 中找到一些额外的内容。它们使用 Python3 编写而成,因此如果你使用 Python2,则需要将super()调用和print函数等内容转换成 Python2 的语法。
1.1 广度优先搜索(Breadth First Search)
让我们使用 Python 实现广度优先搜索。虽然文章主要展示用于搜索算法的 Python 代码,但我们首先需要定义图这个数据结构,以便算法执行。下面是我将要使用的抽象:
- 图(Graph)
一种数据结构:可以告诉我图中每个位置的相邻位置(参看这篇文章)。加权图还可以告诉我沿着边移动的成本。 - 位置(Locations)
一个简单值(整数、字符串、元祖等),用于标记图中的位置。它们不一定是具体地图上的某些位置。根据解决的问题,它们还可能包含其他信息,例如方向、燃料、库存等。 - 搜索(Search)
一种算法:它接受一个图、一个起始位置以及一个目标位置(可选),并为图中的某些位置甚至所有位置计算出一些有用的信息(是否可访问,它的父指针,之间的距离等)。 - 队列(Queue)
搜索算法中用来确定处理图中位置顺序的数据结构。
本文的主要部分,我将专注于搜索算法。在余下的部分,我将逐步填充细节,最终得到一个完整工作的程序。让我们从图开始:
class SimpleGraph:
def __init__(self):
self.edges = {}
def neighbors(self, id):
return self.edges[id]没错,以上就是我们所需的全部代码了!你可能会问:节点(Node)对象在哪里呢?答案是:我很少使用节点对象。我发现使用整数、字符串或元祖来表示位置,然后使用将位置作为索引的数组和哈希表更简单方便。
请注意,边是有方向的:我们可以有一条从A到B的边,但没有从B到A的边。在游戏地图中,大多数情况边都是双向的,但有时也会有单向门或悬崖峭壁用单向边表示。让我们做一个示意图,其中位置为A-E:

对于每一个位置,我需要一个列表来表示它能到达的节点
example_graph = SimpleGraph()
example_graph.edges = {
'A': ['B'],
'B': ['A', 'C', 'D'],
'C': ['A'],
'D': ['E', 'A'],
'E': ['B']
}在我们可以使用搜索算法来处理它之前,我们需要实现一个队列(Queue):
import collections
class Queue:
def __init__(self):
self.elements = collections.deque()
def empty(self):
return len(self.elements) == 0
def put(self, x):
self.elements.append(x)
def get(self):
return self.elements.popleft()该队列类只是内置的collections.deque类的包装。不用担心在你的代码中直接使用deque(译注:这正是 Python 方便之处)。
让我们尝试使用Queue和广度优先搜索算法来处理上文中的示例图:
from implementation import *
def breadth_first_search_1(graph, start):
# print out what we find
frontier = Queue()
frontier.put(start)
visited = {}
visited[start] = True
while not frontier.empty():
current = frontier.get()
print("Visiting %r" % current)
for next in graph.neighbors(current):
if next not in visited:
frontier.put(next)
visited[next] = True
breadth_first_search_1(example_graph, 'A')运行结果:
Visiting 'A'
Visiting 'B'
Visiting 'C'
Visiting 'D'
Visiting 'E'网格(Grids)也可以用图来表示。现在我将定义一个名为 SquareGrid 的图,其中包含位置元组(int,int)。在此地图中,图中的位置(“状态”)与游戏地图上的位置相同,但在许多其他问题中,图中的位置与地图上的位置是不同的。我将不再显示存储边信息,而是使用neighbors函数来计算它们。不过在许多问题中,将它们显示存储更好。
class SquareGrid:
def __init__(self, width, height):
self.width = width
self.height = height
self.walls = []
def in_bounds(self, id):
(x, y) = id
return 0 <= x < self.width and 0 <= y < self.height
def passable(self, id):
return id not in self.walls
def neighbors(self, id):
(x, y) = id
results = [(x + 1, y), (x, y - 1), (x - 1, y), (x, y + 1)]
if (x + y) % 2 == 0: results.reverse()
results = filter(self.in_bounds, results)
results = filter(self.passable, results)
return results让我们尝试使用它处理本文的第一个网格:
from implementation import *
g = SquareGrid(30, 15)
g.walls = DIAGRAM1_WALLS # 长列表, [(21, 0), (21, 2), ...]
draw_grid(g)运行结果:
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . ####. . . . . . . . . . . . . . . . ####. . . . . . .
. . . ####. . . . . . . . ####. . . . . . ####. . . . . . .
. . . ####. . . . . . . . ####. . . . . . ##########. . . .
. . . ####. . . . . . . . ####. . . . . . ##########. . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .为了重建路径,我们需要存储算法是如何到达每一个位置的(即每一个位置的来源),因此我将visited数组(只记录True和False,表明是否已经访问)重命名为came_from(记录位置信息):
from implementation import *
def breadth_first_search_2(graph, start):
# return "came_from"
frontier = Queue()
frontier.put(start)
came_from = {}
came_from[start] = None
while not frontier.empty():
current = frontier.get()
for next in graph.neighbors(current):
if next not in came_from:
frontier.put(next)
came_from[next] = current
return came_from
g = SquareGrid(30, 15)
g.walls = DIAGRAM1_WALLS
parents = breadth_first_search_2(g, (8, 7))
draw_grid(g, width=2, point_to=parents, start=(8, 7))运行结果:
> > > > V V V V V V V V V V V V < < < < < ####V V V V V V V
> > > > > V V V V V V V V V V < < < < < < ####V V V V V V V
> > > > > V V V V V V V V V < < < < < < < ####> V V V V V V
> > ^ ####V V V V V V V V < < < < < < < < ####> > V V V V V
> ^ ^ ####> V V V V V V < ####^ < < < < < ####> > > V V V V
^ ^ ^ ####> > V V V V < < ####^ ^ < < < < ##########V V V <
^ ^ ^ ####> > > V V < < < ####^ ^ ^ < < < ##########V V < <
^ ^ ^ ####> > > A < < < < ####^ ^ ^ ^ < < < < < < < < < < <
V V V ####> > ^ ^ ^ < < < ####^ ^ ^ ^ ^ < < < < < < < < < <
V V V ####> ^ ^ ^ ^ ^ < < ####^ ^ ^ ^ ^ ^ < < < < < < < < <
V V V ####^ ^ ^ ^ ^ ^ ^ < ####^ ^ ^ ^ ^ ^ ^ < < < < < < < <
> V V ####^ ^ ^ ^ ^ ^ ^ ^ ####^ ^ ^ ^ ^ ^ ^ ^ < < < < < < <
> > > > > ^ ^ ^ ^ ^ ^ ^ ^ ####^ ^ ^ ^ ^ ^ ^ ^ ^ < < < < < <
> > > > ^ ^ ^ ^ ^ ^ ^ ^ ^ ####^ ^ ^ ^ ^ ^ ^ ^ ^ ^ < < < < <
> > > ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ####^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ < < < <一些实现使用内部存储(面向对象),创建一个 Node 类,将came_from和其他一些信息存储到类中。相反,我选择使用外部存储,创建一个哈希表(dict)来存储图中所有节点的来源(came_from)。如果你能确定你的地图位置采用整数索引,则可以选择使用数组(list)来存储came_from。
1.2 提前退出(Early Exit)
根据介绍文章的内容,我们要做的仅仅是在主循环中添加一条if语句。这条语句对于广度优先搜索和 Dijkstra 算法是可选的,而对于贪心最佳优先搜索和 A* 算法,这条语句是保证它们效率的必备条件。
from implementation import *
def breadth_first_search_3(graph, start, goal):
frontier = Queue()
frontier.put(start)
came_from = {}
came_from[start] = None
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
if next not in came_from:
frontier.put(next)
came_from[next] = current
return came_from
g = SquareGrid(30, 15)
g.walls = DIAGRAM1_WALLS
parents = breadth_first_search_3(g, (8, 7), (17, 2))
draw_grid(g, width=2, point_to=parents, start=(8, 7), goal=(17, 2))运算结果:
. > > > v v v v v v v v v v v v < . . . . ####. . . . . . .
> > > > > v v v v v v v v v v < < < . . . ####. . . . . . .
> > > > > v v v v v v v v v < < < Z . . . ####. . . . . . .
> > ^ ####v v v v v v v v < < < < < < . . ####. . . . . . .
. ^ ^ ####> v v v v v v < ####^ < < . . . ####. . . . . . .
. . ^ ####> > v v v v < < ####^ ^ . . . . ##########. . . .
. . . ####> > > v v < < < ####^ . . . . . ##########. . . .
. . . ####> > > A < < < < ####. . . . . . . . . . . . . . .
. . . ####> > ^ ^ ^ < < < ####. . . . . . . . . . . . . . .
. . v ####> ^ ^ ^ ^ ^ < < ####. . . . . . . . . . . . . . .
. v v ####^ ^ ^ ^ ^ ^ ^ < ####. . . . . . . . . . . . . . .
> v v ####^ ^ ^ ^ ^ ^ ^ ^ ####. . . . . . . . . . . . . . .
> > > > > ^ ^ ^ ^ ^ ^ ^ ^ ####. . . . . . . . . . . . . . .
> > > > ^ ^ ^ ^ ^ ^ ^ ^ ^ ####. . . . . . . . . . . . . . .
. > > ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ####. . . . . . . . . . . . . . .你可以看到算法在找到目标Z的时候就停止了。
1.3 Dijkstra 算法
下面要开始增加图搜索算法的复杂度了,因为我们将使用比“先进先出(FIFO)”更合适的顺序来处理图中的位置。那么我们需要改变什么呢?
- *图(Graph)*需要知道移动成本
- *队列(Queue)*需要以不同之前的顺序返回节点
- 搜索算法需要从图中读取成本,并跟踪计算成本,将其给到队列
1.3.1 加权图(Graph with weights)
一个普通的图告诉我们每个节点的邻居。一个加权图还告诉我们沿着每条边进行移动的成本。我将添加一个cost(from_node, to_node)函数,该函数告诉我们从位置from_node到to_node之间的成本。在此文使用的图中,为了简化,我选择使运动成本仅依赖于to_node,但是还有其他类型,它们的移动成本依赖于from_node和to_node。另一种实现是将移动成本合并到neighbors函数中。
class GridWithWeights(SquareGrid):
def __init__(self, width, height):
super().__init__(width, height)
self.weights = {}
def cost(self, from_node, to_node):
return self.weights.get(to_node, 1)1.3.2 优先队列(Queue with priorities)
一个优先队列使用“优先级”来组织它的元素。当需要返回一个元素时,它会选择其中优先级最低(也可以是最高的)的那一个元素。
- insert
添加一个元素到队列中 - remove
删除队列中优先级最低的元素 - reprioritize
(可选)将现有元素的优先级改得更低
使用*二叉堆(binary heaps)*可以得到一个快速可靠的优先级队列,但它不支持reprioritize。
译者补充:
二叉堆
二叉堆(英语:binary heap)是一种特殊的堆,二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足堆特性:父节点的键值总是保持固定的序关系于任何一个子节点的键值,且每个节点的左子树和右子树都是一个二叉堆。
当父节点的键值总是大于或等于任何一个子节点的键值时为“最大堆”。当父节点的键值总是小于或等于任何一个子节点的键值时为“最小堆”。
为了得到正确的顺序,我们将使用元组 (优先级,项目)。当插入一个已经在队列中的元素时,我们将得到一个冗余的元素;我将在后文“优化”章节解释为什么这样做是没问题的。
import heapq
class PriorityQueue:
def __init__(self):
self.elements = []
def empty(self):
return len(self.elements) == 0
def put(self, item, priority):
heapq.heappush(self.elements, (priority, item))
def get(self):
return heapq.heappop(self.elements)[1]1.3.3 搜索
这里有一个关于实现的棘手问题:一旦我们考虑移动成本,就会出现一种情况,通过不同的路径访问同一个节点,成本不同,那么就有可能第二次访问一个已经访问过的节点,但是成本更低。这意味着if next not in came_from这行代码不再有用。取而代之,我们必须检查自上次访问这个节点以来成本是否有所下降。(在本文的原始版本中,我没有进行检查,但代码仍然有效;我在这里写了一些关于该错误的注释)
这次使用的地图来自之前的介绍文章:
def dijkstra_search(graph, start, goal):
frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost
frontier.put(next, priority)
came_from[next] = current
return came_from, cost_so_far最终,在搜素完成后,我们需要构建路径:
def reconstruct_path(came_from, start, goal):
current = goal
path = []
while current != start:
path.append(current)
current = came_from[current]
path.append(start) # optional
path.reverse() # optional
return path尽管最好将路径视为由一系列边组成,不过这里将它们存储为一系列节点更为方便。为了构建路径,我们需要从目标节点开始,依据存储在came_from里的数据——指向该节点的前一个节点,不断回溯。当我们到达开始节点时,我们就完成了。不过可以发现,这样构建的路径是反向的(从目标节点到开始节点),因此,如果你想把数据改成正向的,需要在reconstruct_path函数最后调用reverse()方法,将路径反转。有时反向存储更有利,有时将开始节点也加入队列中更有利。
让我们试试看:
from implementation import *
came_from, cost_so_far = dijkstra_search(diagram4, (1, 4), (7, 8))
draw_grid(diagram4, width=3, point_to=came_from, start=(1, 4), goal=(7, 8))
print()
draw_grid(diagram4, width=3, number=cost_so_far, start=(1, 4), goal=(7, 8))
print()
draw_grid(diagram4, width=3, path=reconstruct_path(came_from, start=(1, 4), goal=(7, 8)))运行结果:
v v < < < < < < < <
v v < < < ^ ^ < < <
v v < < < < ^ ^ < <
v v < < < < < ^ ^ .
> A < < < < . . . .
^ ^ < < < < . . . .
^ ^ < < < < < . . .
^ #########^ < v . . .
^ #########v v v Z . .
^ < < < < < < < < .
5 4 5 6 7 8 9 10 11 12
4 3 4 5 10 13 10 11 12 13
3 2 3 4 9 14 15 12 13 14
2 1 2 3 8 13 18 17 14 .
1 A 1 6 11 16 . . . .
2 1 2 7 12 17 . . . .
3 2 3 4 9 14 19 . . .
4 #########14 19 18 . . .
5 #########15 16 13 Z . .
6 7 8 9 10 11 12 13 14 .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
@ @ . . . . . . . .
@ . . . . . . . . .
@ . . . . . . . . .
@ #########. . . . . .
@ #########. . @ @ . .
@ @ @ @ @ @ @ . . .其中if next not in cost_so_far or new_cost < cost_so_far[next]可以简化为if new_cost < cost_so_far.get(next, Infinity),但是我不想过多解释 Python 中的get()用法,所以我就不简化了。另一种方法是使用collections.defaultdict默认为无穷大。
1.4 A* 搜索
贪心最佳优先搜素和 A* 都是用到了一个启发函数。唯一不同是,A* 不仅使用了启发函数还使用 Dijkstra 算法中计算的排序。接下来我将展示 A* 算法:
def heuristic(a, b):
(x1, y1) = a
(x2, y2) = b
return abs(x1 - x2) + abs(y1 - y2)
def a_star_search(graph, start, goal):
frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost + heuristic(goal, next)
frontier.put(next, priority)
came_from[next] = current
return came_from, cost_so_far让我们是这运行它:
from implementation import *
start, goal = (1, 4), (7, 8)
came_from, cost_so_far = a_star_search(diagram4, start, goal)
draw_grid(diagram4, width=3, point_to=came_from, start=start, goal=goal)
print()
draw_grid(diagram4, width=3, number=cost_so_far, start=start, goal=goal)
print()运行结果:
. . . . . . . . . .
. v v v . . . . . .
v v v v < . . . . .
v v v < < . . . . .
> A < < < . . . . .
> ^ < < < . . . . .
> ^ < < < < . . . .
^ #########^ . v . . .
^ #########v v v Z . .
^ < < < < < < < . .
. . . . . . . . . .
. 3 4 5 . . . . . .
3 2 3 4 9 . . . . .
2 1 2 3 8 . . . . .
1 A 1 6 11 . . . . .
2 1 2 7 12 . . . . .
3 2 3 4 9 14 . . . .
4 #########14 . 18 . . .
5 #########15 16 13 Z . .
6 7 8 9 10 11 12 13 . .1.4.1 更直接的路径
如果你在自己的项目中实现这些代码,可能会发现某些路径并不如你所愿。这是正常的。当使用*网格(grid)*时,特别是在移动成本都相同的网格中,最终会遇到一些局限:很多条路径的成本是完全相同的。A* 最终选择了这些路径中的一条,但这通常对你来说并不是最合适的路径。有个快速技巧可以打破这个局限,但并不能达到完美。更好的方式是改变地图的表现形式,这不仅可以使 A* 运行的更快,还可以产生更直接、美观的路径。然而,这些仅适用于移动成本相同的大部分静态地图。对于上文的演示,我使用了快速技巧,但也仅适用于优先级较低的队列。如果你使用的是优先级较高的队列,那么你需要使用其他的技巧。
2 C++ 实现
注意:一些示例代码需要 include redblobgames/pathfinding/a-star/implementation.cpp 才能执行。我使用 C++ 11 编写这些代码,如果你使用的是更老版本的 C++标准,有些代码可能需要更改。
*这里的代码仅供教程参考,不具备正式使用质量。*本文最后一节会给出一些提示来优化它。
2.1 广度优先搜索
让我们在 C++ 中实现广度优先搜索。以下是我们需要用到的组件(与 Python 实现相同):
- 图(Graph)
一种数据结构:可以告诉我图中每个位置的相邻位置(参看这篇文章)。加权图还可以告诉我沿着边移动的成本。 - 位置(Locations)
一个简单值(整数、字符串、元祖等),用于标记图中的位置。它们不一定是具体地图上的某些位置。根据解决的问题,它们还可能包含其他信息,例如方向、燃料、库存等。 - 搜索(Search)
一种算法:它接受一个图、一个起始位置以及一个目标位置(可选),并为图中的某些位置甚至所有位置计算出一些有用的信息(是否可访问,它的父指针,之间的距离等)。 - 队列(Queue)
搜索算法中用来确定处理图中位置顺序的数据结构。
在之前的介绍文章中,我聚焦在搜索上。在这篇文章中,我会填充余下的细节,来使程序完整。让我们从**图(Graph)这个数据结构开始,其中位置(节点)**为char类型:
struct SimpleGraph {
std::unordered_map<char, std::vector<char> > edges;
std::vector<char> neighbors(char id) {
return edges[id];
}
};
这里是一个例子:

SimpleGraph example_graph {{
{'A', {'B'}},
{'B', {'A', 'C', 'D'}},
{'C', {'A'}},
{'D', {'E', 'A'}},
{'E', {'B'}}
}};
C++ 标准库中已经包含了队列类,因此,我们现在已经有了图(SimpleGraph)、位置(char)以及队列(std::queue)。那么让我们来尝试一下广度优先搜索:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
void breadth_first_search(SimpleGraph graph, char start) {
std::queue<char> frontier;
frontier.push(start);
std::unordered_set<char> visited;
visited.insert(start);
while (!frontier.empty()) {
char current = frontier.front();
frontier.pop();
std::cout << "Visiting " << current << '\n';
for (char next : graph.neighbors(current)) {
if (visited.find(next) == visited.end()) {
frontier.push(next);
visited.insert(next);
}
}
}
}
int main() {
breadth_first_search(example_graph, 'A');
}
运行结果:
Visiting A
Visiting B
Visiting C
Visiting D
Visiting E网格(Grid)也可以表示为图。现在,我将定义一个名为 SquareGrid 的图类,其中的位置数据结构为两个整数。在此地图中,图中的位置(“状态”)与游戏地图上的位置相同,但在许多问题中,图中的位置与地图上的位置不同。我将不显式存储边数据,而是使用neighbors函数来计算它们。不过,在其他许多问题中,最好将它们明确存储:
struct GridLocation {
int x, y;
};
namespace std {
/* implement hash function so we can put GridLocation into an unordered_set */
template <> struct hash<GridLocation> {
typedef GridLocation argument_type;
typedef std::size_t result_type;
std::size_t operator()(const GridLocation& id) const noexcept {
return std::hash<int>()(id.x ^ (id.y << 4));
}
};
}
struct SquareGrid {
static std::array<GridLocation, 4> DIRS;
int width, height;
std::unordered_set<GridLocation> walls;
SquareGrid(int width_, int height_)
: width(width_), height(height_) {}
bool in_bounds(GridLocation id) const {
return 0 <= id.x && id.x < width
&& 0 <= id.y && id.y < height;
}
bool passable(GridLocation id) const {
return walls.find(id) == walls.end();
}
std::vector<GridLocation> neighbors(GridLocation id) const {
std::vector<GridLocation> results;
for (GridLocation dir : DIRS) {
GridLocation next{id.x + dir.x, id.y + dir.y};
if (in_bounds(next) && passable(next)) {
results.push_back(next);
}
}
if ((id.x + id.y) % 2 == 0) {
// aesthetic improvement on square grids
std::reverse(results.begin(), results.end());
}
return results;
}
};
std::array<GridLocation, 4> SquareGrid::DIRS =
{GridLocation{1, 0}, GridLocation{0, -1}, GridLocation{-1, 0}, GridLocation{0, 1}};
在辅助文件implementation.cpp我定义了一个函数来生成网格:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
int main() {
SquareGrid grid = make_diagram1();
draw_grid(grid, 2);
}
运行结果:
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . . . . . . . . . . . . . . . . . . . ####. . . . . . .
. . . ####. . . . . . . . . . . . . . . . ####. . . . . . .
. . . ####. . . . . . . . ####. . . . . . ####. . . . . . .
. . . ####. . . . . . . . ####. . . . . . ##########. . . .
. . . ####. . . . . . . . ####. . . . . . ##########. . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . ####. . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .
. . . . . . . . . . . . . ####. . . . . . . . . . . . . . .让我们再实现一遍广度优先搜索,这次带上came_from,对路径持续跟踪:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
template<typename Location, typename Graph>
std::unordered_map<Location, Location>
breadth_first_search(Graph graph, Location start) {
std::queue<Location> frontier;
frontier.push(start);
std::unordered_map<Location, Location> came_from;
came_from[start] = start;
while (!frontier.empty()) {
Location current = frontier.front();
frontier.pop();
for (Location next : graph.neighbors(current)) {
if (came_from.find(next) == came_from.end()) {
frontier.push(next);
came_from[next] = current;
}
}
}
return came_from;
}
int main() {
SquareGrid grid = make_diagram1();
auto parents = breadth_first_search(grid, GridLocation{7, 8});
draw_grid(grid, 2, nullptr, &parents);
}
运行结果:
> > > > v v v v v v v v v v v v < < < < < ####v v v v v v v
> > > > > v v v v v v v v v v < < < < < < ####v v v v v v v
> > > > > v v v v v v v v v < < < < < < < ####> v v v v v v
> > ^ ####v v v v v v v v < < < < < < < < ####> > v v v v v
> ^ ^ ####v v v v v v v < ####^ < < < < < ####> > > v v v v
^ ^ ^ ####v v v v v v < < ####^ ^ < < < < ##########v v v <
^ ^ ^ ####> v v v v < < < ####^ ^ ^ < < < ##########v v < <
v v v ####> > v v < < < < ####^ ^ ^ ^ < < < < < < < < < < <
v v v ####> > * < < < < < ####^ ^ ^ ^ ^ < < < < < < < < < <
v v v ####> ^ ^ ^ < < < < ####^ ^ ^ ^ ^ ^ < < < < < < < < <
v v v ####^ ^ ^ ^ ^ < < < ####^ ^ ^ ^ ^ ^ ^ < < < < < < < <
> v v ####^ ^ ^ ^ ^ ^ < < ####^ ^ ^ ^ ^ ^ ^ ^ < < < < < < <
> > > > > ^ ^ ^ ^ ^ ^ ^ < ####^ ^ ^ ^ ^ ^ ^ ^ ^ < < < < < <
> > > > ^ ^ ^ ^ ^ ^ ^ ^ ^ ####^ ^ ^ ^ ^ ^ ^ ^ ^ ^ < < < < <
> > > ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ####^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ < < < <一些实现使用内部存储(internal storage),创建一个节点(Node)对象来表示图中的节点,通过它来保存came_from和一些其他信息。相反,我选择使用外部存储(external storage),创建一个单独的std::unordered_map来存储图中所有节点的came_from数据。如果你能确定你的图只使用整数来索引节点,那么你还可以使用一维或二维数组 array(或向量 vector)来存储came_from或其他信息。
2.2 提前退出
广度优先搜索和 Dijkstra 算法默认会探索整张地图。如果我们只是寻找某一个目标点,我们可以增加一个判断if (current == goal),一旦我们找到目标点,便立即退出循环。
#include "redblobgames/pathfinding/a-star/implementation.cpp"
template<typename Location, typename Graph>
std::unordered_map<Location, Location>
breadth_first_search(Graph graph, Location start, Location goal) {
std::queue<Location> frontier;
frontier.push(start);
std::unordered_map<Location, Location> came_from;
came_from[start] = start;
while (!frontier.empty()) {
Location current = frontier.front();
frontier.pop();
if (current == goal) {
break;
}
for (Location next : graph.neighbors(current)) {
if (came_from.find(next) == came_from.end()) {
frontier.push(next);
came_from[next] = current;
}
}
}
return came_from;
}
int main() {
GridLocation start{8, 7};
GridLocation goal{17, 2};
SquareGrid grid = make_diagram1();
auto came_from = breadth_first_search(grid, start, goal);
draw_grid(grid, 2, nullptr, &came_from);
}
运行结果:
. > > > v v v v v v v v v v v v < . . . . ####. . . . . . .
> > > > > v v v v v v v v v v < < < . . . ####. . . . . . .
> > > > > v v v v v v v v v < < < < . . . ####. . . . . . .
> > ^ ####v v v v v v v v < < < < < < . . ####. . . . . . .
. ^ ^ ####> v v v v v v < ####^ < < . . . ####. . . . . . .
. . ^ ####> > v v v v < < ####^ ^ . . . . ##########. . . .
. . . ####> > > v v < < < ####^ . . . . . ##########. . . .
. . . ####> > > * < < < < ####. . . . . . . . . . . . . . .
. . . ####> > ^ ^ ^ < < < ####. . . . . . . . . . . . . . .
. . v ####> ^ ^ ^ ^ ^ < < ####. . . . . . . . . . . . . . .
. v v ####^ ^ ^ ^ ^ ^ ^ < ####. . . . . . . . . . . . . . .
> v v ####^ ^ ^ ^ ^ ^ ^ ^ ####. . . . . . . . . . . . . . .
> > > > > ^ ^ ^ ^ ^ ^ ^ ^ ####. . . . . . . . . . . . . . .
> > > > ^ ^ ^ ^ ^ ^ ^ ^ ^ ####. . . . . . . . . . . . . . .
. > > ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ####. . . . . . . . . . . . . . .从结果来看可以发现,现在算法并没有探索整张地图,而是提前结束了。
2.3 Dijkstra 算法
下面要开始增加图搜索算法的复杂度了,因为我们将使用比“先进先出(FIFO)”更合适的顺序来处理图中的位置。那么我们需要改变什么呢?
- *图(Graph)*需要知道移动成本
- *队列(Queue)*需要以不同之前的顺序返回节点
- 搜索算法需要从图中读取成本,并跟踪计算成本,将其给到队列
2.3.1 加权图
一个普通的图告诉我们每个节点的邻居。一个加权图还告诉我们沿着每条边进行移动的成本。我将添加一个cost(from_node, to_node)函数,该函数告诉我们从位置from_node到to_node之间的成本。在此文使用的图中,为了简化,我选择使运动成本仅依赖于to_node,但是还有其他类型,它们的移动成本依赖于from_node和to_node。另一种实现是将移动成本合并到neighbors函数中。这里是一个网格图,其中有一些节点的移动成本是5:
struct GridWithWeights: SquareGrid {
std::unordered_set<GridLocation> forests;
GridWithWeights(int w, int h): SquareGrid(w, h) {}
double cost(GridLocation from_node, GridLocation to_node) const {
return forests.find(to_node) != forests.end()? 5 : 1;
}
};
1.3.2 优先队列(Queue with priorities)
我们需要优先队列。C++ 提供了一个priority_queue类,它使用了二叉堆,因此不能为元素重新设置优先级。我将使用 pair(priority,item)作为队列元素,进行排序。C++ 优先队列默认返回优先级最大的元素,使用的是std::less比较符,但是,我们需要的是最小的元素,因此,使用std::greater比较符。
template<typename T, typename priority_t>
struct PriorityQueue {
typedef std::pair<priority_t, T> PQElement;
std::priority_queue<PQElement, std::vector<PQElement>,
std::greater<PQElement>> elements;
inline bool empty() const {
return elements.empty();
}
inline void put(T item, priority_t priority) {
elements.emplace(priority, item);
}
T get() {
T best_item = elements.top().second;
elements.pop();
return best_item;
}
};
在上面的代码中,我对 C++ std::priority_queue 封装了一层,但我认为直接使用该类也很合理。
1.3.3 搜索
template<typename Location, typename Graph>
void dijkstra_search
(Graph graph,
Location start,
Location goal,
std::unordered_map<Location, Location>& came_from,
std::unordered_map<Location, double>& cost_so_far)
{
PriorityQueue<Location, double> frontier;
frontier.put(start, 0);
came_from[start] = start;
cost_so_far[start] = 0;
while (!frontier.empty()) {
Location current = frontier.get();
if (current == goal) {
break;
}
for (Location next : graph.neighbors(current)) {
double new_cost = cost_so_far[current] + graph.cost(current, next);
if (cost_so_far.find(next) == cost_so_far.end()
|| new_cost < cost_so_far[next]) {
cost_so_far[next] = new_cost;
came_from[next] = current;
frontier.put(next, new_cost);
}
}
}
}
成本变量的类型应完全与图中的类型匹配。如果你使用int,则你可以将int作为成本变量类型以及优先级队列中的优先级;如果你使用double,则成本变量类型和优先级队列中的优先级应相应使用double,诸如此类。在这段代码中,我使用了double,但我也可以使用int,它们的工作原理是相同的。但是,如果你的边成本是浮点型,或者你的启发函数是浮点型,那么在这里你也必须使用浮点型。
最终,在搜素完成后,我们需要构建路径:
template<typename Location>
std::vector<Location> reconstruct_path(
Location start, Location goal,
std::unordered_map<Location, Location> came_from
) {
std::vector<Location> path;
Location current = goal;
while (current != start) {
path.push_back(current);
current = came_from[current];
}
path.push_back(start); // optional
std::reverse(path.begin(), path.end());
return path;
}
尽管最好将路径视为由一系列边组成,不过这里将它们存储为一系列节点更为方便。为了构建路径,我们需要从目标节点开始,依据存储在came_from里的数据——指向该节点的前一个节点,不断回溯。当我们到达开始节点时,我们就完成了。不过可以发现,这样构建的路径是反向的(从目标节点到开始节点),因此,如果你想把数据改成正向的,需要在reconstruct_path函数最后调用reverse()方法,将路径反转。有时反向存储更有利,有时将开始节点也加入队列中更有利。
让我们试试看:
#include "redblobgames/pathfinding/a-star/implementation.cpp"
int main() {
GridWithWeights grid = make_diagram4();
GridLocation start{1, 4};
GridLocation goal{8, 5};
std::unordered_map<GridLocation, GridLocation> came_from;
std::unordered_map<GridLocation, double> cost_so_far;
dijkstra_search(grid, start, goal, came_from, cost_so_far);
draw_grid(grid, 2, nullptr, &came_from);
std::cout << '\n';
draw_grid(grid, 3, &cost_so_far, nullptr);
std::cout << '\n';
std::vector<GridLocation> path = reconstruct_path(start, goal, came_from);
draw_grid(grid, 3, nullptr, nullptr, &path);
}
运行结果:
v v < < < < < < < <
v v < < < ^ ^ < < <
v v < < < < ^ ^ < <
v v < < < < < ^ ^ <
> * < < < < < > ^ <
^ ^ < < < < . v ^ .
^ ^ < < < < < v < .
^ ######^ < v v < .
^ ######v v v < < <
^ < < < < < < < < <
5 4 5 6 7 8 9 10 11 12
4 3 4 5 10 13 10 11 12 13
3 2 3 4 9 14 15 12 13 14
2 1 2 3 8 13 18 17 14 15
1 0 1 6 11 16 21 20 15 16
2 1 2 7 12 17 . 21 16 .
3 2 3 4 9 14 19 16 17 .
4 #########14 19 18 15 16 .
5 #########15 16 13 14 15 16
6 7 8 9 10 11 12 13 14 15
. @ @ @ @ @ @ . . .
. @ . . . . @ @ . .
. @ . . . . . @ @ .
. @ . . . . . . @ .
. @ . . . . . . @ .
. . . . . . . . @ .
. . . . . . . . . .
. #########. . . . . .
. #########. . . . . .
. . . . . . . . . .结果与 Python 版本并不完全相同,因为我使用的都是它们内置的优先级队列,而 C++ 和 Python 可能会对相同优先级的节点进行不同的排序。
A* 搜索
A* 算法几乎和 Dijkstra 算法一样,只不过我们添加了一个启发函数。请注意,该算法并不只针对网格地图。关于网格的信息在图类型(SquareGrids)、位置类(Location结构)以及heuristic函数中。将它们3个替换掉,你可以将 A* 算法与任意其他图数据结构结合在一起使用。
inline double heuristic(GridLocation a, GridLocation b) {
return std::abs(a.x - b.x) + std::abs(a.y - b.y);
}
template<typename Location, typename Graph>
void a_star_search
(Graph graph,
Location start,
Location goal,
std::unordered_map<Location, Location>& came_from,
std::unordered_map<Location, double>& cost_so_far)
{
PriorityQueue<Location, double> frontier;
frontier.put(start, 0);
came_from[start] = start;
cost_so_far[start] = 0;
while (!frontier.empty()) {
Location current = frontier.get();
if (current == goal) {
break;
}
for (Location next : graph.neighbors(current)) {
double new_cost = cost_so_far[current] + graph.cost(current, next);
if (cost_so_far.find(next) == cost_so_far.end()
|| new_cost < cost_so_far[next]) {
cost_so_far[next] = new_cost;
double priority = new_cost + heuristic(next, goal);
frontier.put(next, priority);
came_from[next] = current;
}
}
}
}
priority值的类型,包括优先级队列中使用的类型,必须最够大,大到可以包含图中移动成本(cost_t)和启发函数值。例如,如果图成本为整数,且启发函数返回双精度,则优先级队列也必须接受双精度值。在上述示例代码中,我对这三个值(成本费用,启发式函数和优先级)统一使用了double,不过我也可以使用int,因为我的费用成本和启发式函数都是整数值。
小提示:写frontier.put(start, heuristic(start, goal))比写frontier.put(start, 0)更正确,但是这里没有区别,因为起始节点的优先级无关紧要。开始时,它是优先级队列中唯一的节点,一定会被优先访问并从队列中删除。
#include "redblobgames/pathfinding/a-star/implementation.cpp"
int main() {
GridWithWeights grid = make_diagram4();
GridLocation start{1, 4};
GridLocation goal{8, 5};
std::unordered_map<GridLocation, GridLocation> came_from;
std::unordered_map<GridLocation, double> cost_so_far;
a_star_search(grid, start, goal, came_from, cost_so_far);
draw_grid(grid, 2, nullptr, &came_from);
std::cout << '\n';
draw_grid(grid, 3, &cost_so_far, nullptr);
std::cout << '\n';
std::vector<GridLocation> path = reconstruct_path(start, goal, came_from);
draw_grid(grid, 3, nullptr, nullptr, &path);
}
运行结果:
v v v v < < < < < <
v v v v < ^ ^ < < <
v v v v < < ^ ^ < <
v v v < < < . ^ ^ <
> * < < < < . > ^ <
> ^ < < < < . . ^ .
^ ^ ^ < < < . . . .
^ ######^ . . . . .
^ ######. . . . . .
^ . . . . . . . . .
5 4 5 6 7 8 9 10 11 12
4 3 4 5 10 13 10 11 12 13
3 2 3 4 9 14 15 12 13 14
2 1 2 3 8 13 . 17 14 15
1 0 1 6 11 16 . 20 15 16
2 1 2 7 12 17 . . 16 .
3 2 3 4 9 14 . . . .
4 #########14 . . . . .
5 #########. . . . . .
6 . . . . . . . . .
. . . @ @ @ @ . . .
. . . @ . . @ @ . .
. . . @ . . . @ @ .
. . @ @ . . . . @ .
. @ @ . . . . . @ .
. . . . . . . . @ .
. . . . . . . . . .
. #########. . . . . .
. #########. . . . . .
. . . . . . . . . .1.4.1 更直接的路径
如果你在自己的项目中实现这些代码,可能会发现某些路径并不如你所愿。这是正常的。当使用*网格(grid)*时,特别是在移动成本都相同的网格中,最终会遇到一些局限:很多条路径的成本是完全相同的。A* 最终选择了这些路径中的一条,但这通常对你来说并不是最合适的路径。有个快速技巧可以打破这个局限,但并不能达到完美。更好的方式是改变地图的表现形式,这不仅可以使 A* 运行的更快,还可以产生更直接、美观的路径。然而,这些仅适用于移动成本相同的大部分静态地图。对于上文的演示,我使用了快速技巧,但也仅适用于优先级较低的队列。如果你使用的是优先级较高的队列,那么你需要使用其他的技巧。
2.5 生产力代码
上面展示的 C++ 代码经过简化,可以更轻松地展示算法和数据结构。然而,在实践中,你需要做很多不同的事情:
- 内联(inline)短小函数
- Location参数应该是Graph的一部分
- 费用成本可以为int或double,并且应该是Graph的一部分
- 如果图节点索引是密集整数,使用array而不是unordered_set,并且在退出时重制这些值,而不是在进入的时候初始化
- 使用引用传递内存大的数据结构,而不是值传递
- 通过参数(out parameters)返回内存大的数据结构,而不是直接return它,或者使用移动构造函数(move constructors)(举个例子,neighbors函数返回vector)
- 启发式函数易变化,应该成为 A* 函数的一个模版参数,这样可以进行内联
以下函数展示了上述这些变化(但不是全部):
template<typename Graph>
void a_star_search
(Graph graph,
typename Graph::Location start,
typename Graph::Location goal,
std::function<typename Graph::cost_t(typename Graph::Location a, typename Graph::Location b)> heuristic,
std::unordered_map<typename Graph::Location, typename Graph::Location>& came_from,
std::unordered_map<typename Graph::Location, typename Graph::cost_t>& cost_so_far)
{
typedef typename Graph::Location Location;
typedef typename Graph::cost_t cost_t;
PriorityQueue<Location, cost_t> frontier;
std::vector<Location> neighbors;
frontier.put(start, cost_t(0));
came_from[start] = start;
cost_so_far[start] = cost_t(0);
while (!frontier.empty()) {
typename Location current = frontier.get();
if (current == goal) {
break;
}
graph.get_neighbors(current, neighbors);
for (Location next : neighbors) {
cost_t new_cost = cost_so_far[current] + graph.cost(current, next);
if (cost_so_far.find(next) == cost_so_far.end()
|| new_cost < cost_so_far[next]) {
cost_so_far[next] = new_cost;
cost_t priority = new_cost + heuristic(next, goal);
frontier.put(next, priority);
came_from[next] = current;
}
}
}
}
我希望本文代码更多展示数据结构和算法,而不是展示 C++ 优化,所以我努力简化代码,不是写运行更快或更抽象的代码。
3 C# 实现
这些是我的第一个 C# 程序,因此它们可能不是常见写法或符合 C# 风格。这些示例虽然不如 Python 和 C++ 部分完整,但希望对您有所帮助。
下面是简单图和广度优先搜索:
using System;
using System.Collections.Generic;
public class Graph<Location>
{
// NameValueCollection would be a reasonable alternative here, if
// you're always using string location types
public Dictionary<Location, Location[]> edges
= new Dictionary<Location, Location[]>();
public Location[] Neighbors(Location id)
{
return edges[id];
}
};
class BreadthFirstSearch
{
static void Search(Graph<string> graph, string start)
{
var frontier = new Queue<string>();
frontier.Enqueue(start);
var visited = new HashSet<string>();
visited.Add(start);
while (frontier.Count > 0)
{
var current = frontier.Dequeue();
Console.WriteLine("Visiting {0}", current);
foreach (var next in graph.Neighbors(current))
{
if (!visited.Contains(next)) {
frontier.Enqueue(next);
visited.Add(next);
}
}
}
}
static void Main()
{
Graph<string> g = new Graph<string>();
g.edges = new Dictionary<string, string[]>
{
{ "A", new [] { "B" } },
{ "B", new [] { "A", "C", "D" } },
{ "C", new [] { "A" } },
{ "D", new [] { "E", "A" } },
{ "E", new [] { "B" } }
};
Search(g, "A");
}
}
下面是加权网格图的实现:
using System;
using System.Collections.Generic;
// A* needs only a WeightedGraph and a location type L, and does *not*
// have to be a grid. However, in the example code I am using a grid.
public interface WeightedGraph<L>
{
double Cost(Location a, Location b);
IEnumerable<Location> Neighbors(Location id);
}
public struct Location
{
// Implementation notes: I am using the default Equals but it can
// be slow. You'll probably want to override both Equals and
// GetHashCode in a real project.
public readonly int x, y;
public Location(int x, int y)
{
this.x = x;
this.y = y;
}
}
public class SquareGrid : WeightedGraph<Location>
{
// Implementation notes: I made the fields public for convenience,
// but in a real project you'll probably want to follow standard
// style and make them private.
public static readonly Location[] DIRS = new []
{
new Location(1, 0),
new Location(0, -1),
new Location(-1, 0),
new Location(0, 1)
};
public int width, height;
public HashSet<Location> walls = new HashSet<Location>();
public HashSet<Location> forests = new HashSet<Location>();
public SquareGrid(int width, int height)
{
this.width = width;
this.height = height;
}
public bool InBounds(Location id)
{
return 0 <= id.x && id.x < width
&& 0 <= id.y && id.y < height;
}
public bool Passable(Location id)
{
return !walls.Contains(id);
}
public double Cost(Location a, Location b)
{
return forests.Contains(b) ? 5 : 1;
}
public IEnumerable<Location> Neighbors(Location id)
{
foreach (var dir in DIRS) {
Location next = new Location(id.x + dir.x, id.y + dir.y);
if (InBounds(next) && Passable(next)) {
yield return next;
}
}
}
}
public class PriorityQueue<T>
{
// I'm using an unsorted array for this example, but ideally this
// would be a binary heap. There's an open issue for adding a binary
// heap to the standard C# library: https://github.com/dotnet/corefx/issues/574
//
// Until then, find a binary heap class:
// * https://github.com/BlueRaja/High-Speed-Priority-Queue-for-C-Sharp
// * http://visualstudiomagazine.com/articles/2012/11/01/priority-queues-with-c.aspx
// * http://xfleury.github.io/graphsearch.html
// * http://stackoverflow.com/questions/102398/priority-queue-in-net
private List<Tuple<T, double>> elements = new List<Tuple<T, double>>();
public int Count
{
get { return elements.Count; }
}
public void Enqueue(T item, double priority)
{
elements.Add(Tuple.Create(item, priority));
}
public T Dequeue()
{
int bestIndex = 0;
for (int i = 0; i < elements.Count; i++) {
if (elements[i].Item2 < elements[bestIndex].Item2) {
bestIndex = i;
}
}
T bestItem = elements[bestIndex].Item1;
elements.RemoveAt(bestIndex);
return bestItem;
}
}
/* NOTE about types: in the main article, in the Python code I just
* use numbers for costs, heuristics, and priorities. In the C++ code
* I use a typedef for this, because you might want int or double or
* another type. In this C# code I use double for costs, heuristics,
* and priorities. You can use an int if you know your values are
* always integers, and you can use a smaller size number if you know
* the values are always small. */
public class AStarSearch
{
public Dictionary<Location, Location> cameFrom
= new Dictionary<Location, Location>();
public Dictionary<Location, double> costSoFar
= new Dictionary<Location, double>();
// Note: a generic version of A* would abstract over Location and
// also Heuristic
static public double Heuristic(Location a, Location b)
{
return Math.Abs(a.x - b.x) + Math.Abs(a.y - b.y);
}
public AStarSearch(WeightedGraph<Location> graph, Location start, Location goal)
{
var frontier = new PriorityQueue<Location>();
frontier.Enqueue(start, 0);
cameFrom[start] = start;
costSoFar[start] = 0;
while (frontier.Count > 0)
{
var current = frontier.Dequeue();
if (current.Equals(goal))
{
break;
}
foreach (var next in graph.Neighbors(current))
{
double newCost = costSoFar[current]
+ graph.Cost(current, next);
if (!costSoFar.ContainsKey(next)
|| newCost < costSoFar[next])
{
costSoFar[next] = newCost;
double priority = newCost + Heuristic(next, goal);
frontier.Enqueue(next, priority);
cameFrom[next] = current;
}
}
}
}
}
public class Test
{
static void DrawGrid(SquareGrid grid, AStarSearch astar) {
// Print out the cameFrom array
for (var y = 0; y < 10; y++)
{
for (var x = 0; x < 10; x++)
{
Location id = new Location(x, y);
Location ptr = id;
if (!astar.cameFrom.TryGetValue(id, out ptr))
{
ptr = id;
}
if (grid.walls.Contains(id)) { Console.Write("##"); }
else if (ptr.x == x+1) { Console.Write("\u2192 "); }
else if (ptr.x == x-1) { Console.Write("\u2190 "); }
else if (ptr.y == y+1) { Console.Write("\u2193 "); }
else if (ptr.y == y-1) { Console.Write("\u2191 "); }
else { Console.Write("* "); }
}
Console.WriteLine();
}
}
static void Main()
{
// Make "diagram 4" from main article
var grid = new SquareGrid(10, 10);
for (var x = 1; x < 4; x++)
{
for (var y = 7; y < 9; y++)
{
grid.walls.Add(new Location(x, y));
}
}
grid.forests = new HashSet<Location>
{
new Location(3, 4), new Location(3, 5),
new Location(4, 1), new Location(4, 2),
new Location(4, 3), new Location(4, 4),
new Location(4, 5), new Location(4, 6),
new Location(4, 7), new Location(4, 8),
new Location(5, 1), new Location(5, 2),
new Location(5, 3), new Location(5, 4),
new Location(5, 5), new Location(5, 6),
new Location(5, 7), new Location(5, 8),
new Location(6, 2), new Location(6, 3),
new Location(6, 4), new Location(6, 5),
new Location(6, 6), new Location(6, 7),
new Location(7, 3), new Location(7, 4),
new Location(7, 5)
};
// Run A*
var astar = new AStarSearch(grid, new Location(1, 4),
new Location(8, 5));
DrawGrid(grid, astar);
}
}
4 算法变体
本文中的 Dijkstra 算法和 A* 算法与常见 AI 课本上的算法略有不同。
纯粹的 Dijkstra 算法会将全部节点添加到优先级队列开始,并且没有提前退出逻辑。它在队列中使用“减小键(decrease-key)”的操作。理论上没问题,但是在实践中...
- 通过启动时优先级队列只包含起始节点,我们可以保证队列很小,这可以提高运行效率、减小内存使用。
- 使用提前退出,我们几乎不需要将所有节点都插入优先级队列中,并且一旦我们找到目标立即返回路径。
- 通过一开始不将所有节点都加入队列中,大多数时间我们可以使用性能更好的插入操作,而不是性能更差的减小键(decrease-key)操作。
- 通过一开始不将所有节点都加入队列中,我们可以处理无法得知图中所有节点,或者图中由无穷多个节点这些情况。
这个变体有时被称为“统一成本搜索(Uniform Cost Search)”。请参阅维基百科以查看伪代码,或阅读Felner的论文[PDF]来查看这些更改的依据。
伪代码如下:
procedure uniform_cost_search(Graph, start, goal) is node ← start cost ← 0 frontier ← priority queue containing node only explored ← empty set do if frontier is empty then return failure node ← frontier.pop() if node is goal then return solution explored.add(node) for each of node's neighbors n do if n is not in explored then frontier.add(n)
我的版本与你可能在其他地方找到的版本之间还有三个不同之处。这些变化适用于 Dijkstra 算法和 A* 算法:
- 我省去了检查节点是否处于边界队列中且成本更高。这样,我最终在边界队列中得到了重复的元素。不过该算法仍然有效。它将重新访问某些必要位置(但根据我的经验,只要启发函数合理,很少出现这种情况)。这样代码更为简单,它也使我可以使用更简单、更快速的优先级队列,尽管该队列不支持减少键操作。论文“优先级队列和 Dijkstra 的算法”表明,这种方法在实践中速度更快。
- 我没有存储“封闭集(closed set)”和“开放集(open set)”,而是用一个visited来告诉我它是否在这些集合中。这进一步简化了代码。
- 我不需要单独显式存储的开放集或封闭集合,因为came_from和cost_so_far表的键隐式包含了这些信息。由于我们总是需要这两个表之一,因此无需再分别存储开放/封闭集合。
- 我使用哈希表而不是节点对象的数组。这消除了许多其他实现中相当耗时的初始化步骤。对于大型游戏地图,这些数组的初始化通常比 A* 的其余部分慢。
如果你有更多建议可以简化并保持性能,请让我知道!
5 优化
对于本文展现的代码,我一直专注于简单性和通用性,而不是性能。首先让它运行起来,然后再让它运行更快。我在实际项目中使用的许多优化方式都是特定于该项目的,因此,除了提供最佳代码外,这里还有一些针对你自己的项目的一些想法:
5.1 图
你能做到的最大优化就是探索更少的节点。我的第一条建议是,如果你使用的是网格图,请考虑使用非网格寻路图。这并不总是可行的,但值得尝试。
如果你的图结构简单(例如网格),请使用函数计算邻居。如果是更复杂的结构(非网格或具有大量墙壁的网格,如迷宫),则直接将邻居存储在数据结构中。
你还可以通过复用邻居数组来节省一些复制。不必每次都返回一个新值,而是在搜索代码中分配一次,然后将其传递到图的neighbors方法中。
5.2 队列
广度优先搜索只需使用简单队列而不是其他算法中所需的优先级队列。简单队列比优先级队列更简单、更快。作为交换,其他算法通常只需探索更少的节点。在大多数游戏地图中,探索更少的节点比其他算法带来的性能消耗更值得。不过还是有些地图,从节点上你没办法节省很多耗时,那么最好使用广度优先搜索。
对于队列,请使用双端队列(deque)而不是数组(array)。双端队列允许在任一端快速插入和移除,而数组仅能在一端快速插入。在 Python 中,请参阅collections.deque;在 C++ 中,请参阅deque容器。然而,广度优先搜索甚至不需要队列;它可以使用两个向量,当其中一个为空时交换它们。
对于优先级队列,请使用二叉堆(binary heap)而不是数组(array)或排序数组(sorted array)。二叉堆允许快速插入和删除,而数组只能在其中一个操作上很快。在 Python 中,请参见heapq;在 C++ 中,请参见priority_queue容器。
在 Python 中,我上面展示的Queue和PriorityQueue类非常简单,你甚至可以考虑将这些方法内联到搜索算法中。不过,我不知道这样能带来多大的性能提升?我需要测试一下。C++ 版本将被内联。
在 Dijkstra 算法中,请注意,优先级队列中的优先级存储了两遍,一遍存储在优先级队列中,一遍存储在cost_so_far中,因此你可以编写一个优先级队列以从其他地方获取优先级。不过,我不确定这样做是否值得。
Chen,Chowdhury,Ramachandran,Lan Roche 和 Tong 撰写的论文“ Priority Queues and Dijkstra's Algorithm”建议不要重新设置优先级,以此来优化 Dijkstra 算法的结构,还建议研究配对堆(pairing heaps)和其他数据结构。
如果你考虑使用二叉堆以外的数据结构,请首先测量边界的大小和重新计算优先级的频率。分析代码,查看优先级队列是否为瓶颈。
我的直觉是,分桶(bucketing)很有前途。就像当键是整数时,桶排序和基数排序可以作为快速排序的替代方法一样,在此情况下,Dijkstra 算法和 A* 算法表现甚至更好。Dijkstra 算法的优先级范围非常窄。如果队列中最低优先级为f,那么最高优先级就为f+e,其中e为边中最大的权重。在上文示例中,我们边的权重为1和5。这意味着队列中所有优先级都介于f和f+5之间。由于它们都是整数,因此一共只有6个不同的优先级。我们可以使用6个桶,根本不用进行任何排序!A* 具有更宽泛的优先级,但仍值得一试。并且还有更先进的桶研究来处理宽泛的情况。
请注意,如果所有边的权重均为1,则优先级将全部在f和f+1之间。这产生了广度优先搜索的变体,该变体使用两个数组而不是队列,而这正是我在六边形网格文章中使用的。如果权重为1或2,则将有三个数组;如果权重为1、2或3,则将有四个数组;等等。
5.3 搜索
启发式函数增加了复杂性和cpu耗时。不过,目标是探索更少的节点。在某些地图(例如迷宫)中,启发式函数可能不会带来太多有用信息,最好使用没有启发式函数的简单算法。
某些人使用不可接受(高估)的启发函数(inadmissible heuristic)来加快 A* 搜索。这似乎是合理的。不过,我尚未仔细研究过它。我相信(但不确定),即使已将某些已访问过的节点从边界队列中移除,也可能需要再次访问它。
某些实现总是将新节点插入到开放集中,即使该节点已经存在其中也是如此。这样你可以避免检查节点是否已经在开放集中这种潜在高耗时的步骤。不过,这也将使你的开放集更大/更慢,并且最终需要评估更多的节点。如果开放集检测非常耗时,那么这样做仍然是值得的。不过,在我提供的代码中,我降低了测试成本,并且不使用这种方法。
某些实现不判断开放集中的新节点是否比现有节点更好。这避免了潜在的耗时检查。但是,它也可能导致产生一个bug。对于某些类型的地图,跳过此判断将找不到最短的路径。在我提供的代码中,我对此进行了检查(new_cost < cost_so_far)。该测试性能很好,因为我使查找cost_so_far很高效。
5.4 整数位置
如果你的图使用整数作为位置索引,请考虑使用简单数组而不是哈希表来实现cost_so_far、visited、came_from等。由于visited是布尔数组,因此可以使用位(bit)向量。初始化所有位置索引对应的visited位,但不需要初始化cost_so_far和came_from。然后仅在第一次访问它们时进行初始化。
vector<uint16_t> visited(1 + maximum_node_id/16);
…
size_t index = node_id/16;
uint16_t bitmask = 1u << (node_id & 0xf);
if (!(visited[index] & bitmask)
|| new_cost < cost_so_far[next]) {
visited[index] |= bitmask;
…
}如果一次只运行一个搜索,则可以静态分配这些数组,在不同调用间复用这些数组。然后保留一个记录所有已分配给位向量的索引的数组,最后在退出时将其重置。例如:
static vector<uint16_t> visited(1 + maximum_node_id/16);
static vector<size_t> indices_to_clear;
…
size_t index = node_id/16;
uint16_t bitmask = 1u << (node_id & 0xf);
if (!(visited[index] & bitmask)
|| new_cost < cost_so_far[next]) {
if (!visited[index]) {
indices_to_clear.push_back(index);
}
visited[index] |= bitmask;
…
}
…
for (size_t index : indices_to_clear) {
visited[index] = 0;
}
indices_to_clear.clear();(注意:我尚未使用或测试此代码)
常见问题
6.1 错误的路径
如果你没有得到最短的路径,请尝试测试:
- 你的优先级队列工作正常吗?尝试停止搜索并使所有元素出队。他们都应该按照正确的优先级排序。
- 你的启发式函数是否曾经高估了真实距离?除非你高估了距离,否则新节点的优先级永远不能低于其父节点的优先级(你可以这样做,但不会再得到最短路径了)。
- 在静态类型的语言中,费用成本、启发式函数和优先级值需要互相兼容类型。本文中的示例代码适用于整数或浮点类型,但并非所有图和启发式函数都限制为整数值。由于优先级是费用成本和启发式函数值的总和,因此如果费用成本或启发式函数值是浮点数,则优先级将需要为浮点数。
6.1 不美观的路径
当人们在网格上运行 A* 时,最常见的问题是为什么我的路径看起来不够直接?如果你告诉 A* 所有网格运动成本都是相等的,那么就会有很多相同长度的最短路径,并且算法会任意选择一条。虽然路径很短,但看起来并不好。
- 一种解决方案是得到路径后使用“string pulling”算法进行优化。
- 一种解决方案是正确的方向上引导路径,通过调整启发式函数。这里有些小技巧,但不能在所有情况下都有效;在这里阅读更多。
- 一种解决方案是不使用网格。只告诉 A* 可能会转弯的地方,而不是每个网格正方形。在这里阅读更多。
- 一种解决方案是取巧,但有时它会起作用。当遍历邻居时,不要总是使用相同的顺序(例如北,东,南,西),改变“奇数”网格节点(其中(x + y)% 2 == 1的那些)的顺序。我在我的这些教程页面上使用了这个技巧。
7 相关阅读
- Aleksander Nowak 编写了此代码的Go版本,地址:https://github.com/vyrwu/a-star-redblob
- 算法教科书通常使用带有单字母变量名称的数学符号。在这些页面中,我尝试使用更具描述性的变量名。对应关系:
- cost有时写作w、d、l、length
- cost_so_far常写作g、d、distance
- heuristic常写作h
- 在 A* 中,priority常写作f,f = g + h
- came_from有时写作π、parent、previous、prev
- frontier常被称为 OPEN
- visited 为 OPEN 和 CLOSED 的联合
- 位置,比如current和next被称为states写作u、v
完。
目录