撰写了文章更新于 2020-04-01 11:45:50

从C#开始的编程入门——二叉树

如果你玩过头图这个游戏，那么你已经见过二叉树了。

在这篇文章中，我们运用前面所学，实现计算机科学中应用非常广泛的一种数据结构，二叉树。一些二叉树衍生出的数据结构可以用来支持很多算法，比如二叉搜索树。不过我这里我们只介绍最简单没有什么特殊性质的二叉树。因此也不需要惊慌。

什么是二叉树

二叉树是一种树，由节点（node）相互连接而成。二叉树的每个节点最多有两个子节点（child），一般称作左右孩子节点。每个节点最多有一个父节点（parent），没有父节点的节点通常被称为根（root）。而没有子节点的节点，被称为叶（leaf）。和真实的树相比，表示数据结构的示意图通常会倒过来画。

递归定义

一棵二叉树中任意一个或者相连的多个节点我们也可以看作是一棵子树。这样一来就是树中有树中有树中有树。我们定义二叉树类的时候我们也就不需要考虑一个单独的节点类，而是把所有节点都当作树看就行了。

由于我们定义的是一种抽象数据结构，我们的二叉树必然是一个范型类型。T代表每个节点的数据类型。不过由于我们这里定义的是非常单纯的二叉树没有任何特点，我们也就公开所有属性，要注意防止某个属性的引用断掉而找不到了。

public class BinaryTree<T>
{
   public T Value {set;get;}
   public BinaryTree<T> Left {set;get;}
   public BinaryTree<T> Right {set;get;}

   public BinaryTree(T value, BinaryTree<T> left = null, BinaryTree<T> right = null)
    {
        Value = value;
        Left = left;
        Right = right;
    }
}

一棵普通二叉树也就没有其它特别的方法了。如果有机会我可能会补充二叉搜索树，二叉搜索树对节点的位置有严格的要求，因此插入节点和删除节点也有特定的算法。

遍历与枚举器

遍历(traverse)，简单来说就是挨个节点走一遍。从另一种角度来说就是枚举树中的每个节点。也就是说，我们要实现一个枚举器，让二叉树实现可枚举接口。

二叉树有很多分支，因此遍历的顺序不是单一的。通常有三种顺序，称为前序、中序、后序（pre-order、in-order、post-order）。也就是说对于一个有两个孩子的节点，是中左右，还是左中右，又或是左右中。我们这里实现中序做示范。

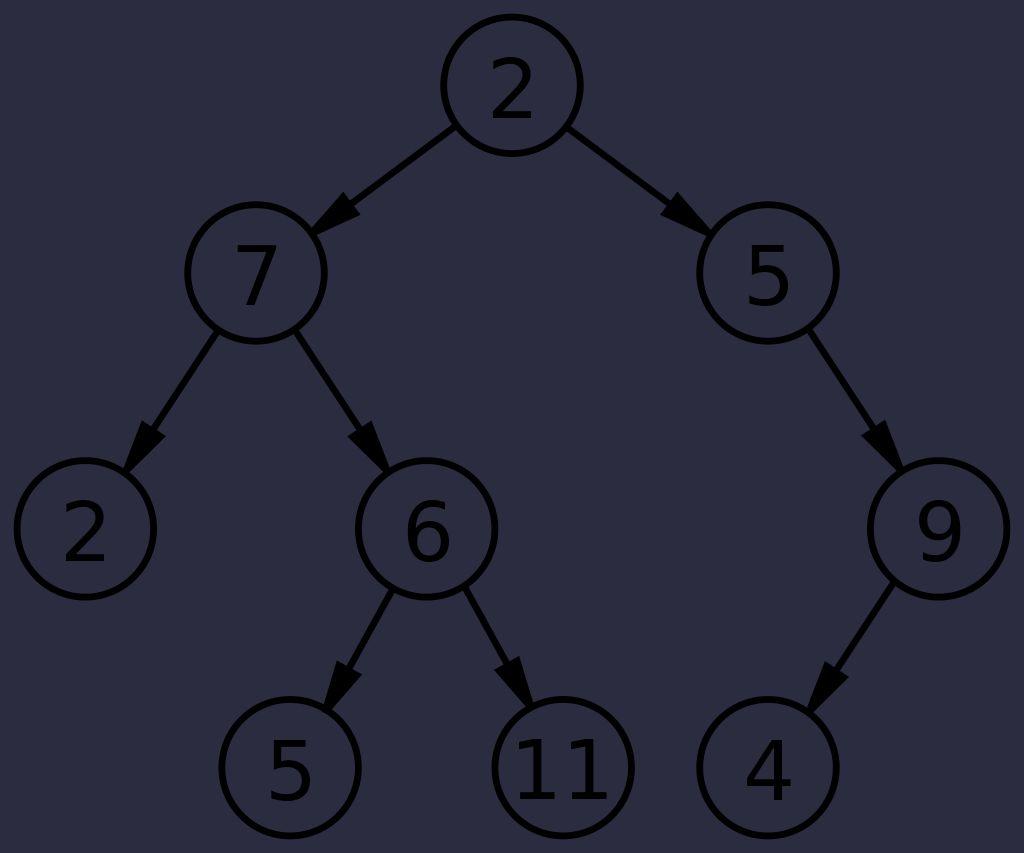
中序遍历首先找到“最左边”的节点。也就是我们要不断访问左孩子直到找到一个节点没有左孩子，这里也就是2。.然后，回到这个子树的中间节点，也就是7，然后遍历它的右子树，也就是油在右边重复这个过程，最终中序遍历的顺序是：2，7，5，6，11，2，5，4，9。

由于在遍历过程中我们需要回到上一层的节点，因此我们需要记录位置才行。如果在枚举器中使用递归算法，那么很难记录相对位置，因此我们这里采用一种投机取巧的办法，事先把节点遍历的顺序安排好。

我们先实现枚举器：

public struct BinaryTreeEnumerator : IEnumerator
{
    private BinaryTree root;
    private BinaryTree currentNode;
    private Queue> nodes;
// ……

首先我们进行声明，实现范型IEnumerator接口。定义三个字段，root代表我们迭代起始处，currentNode是当前的节点。nodes是我们用来记录遍历顺序的一个队列。

private void InOrderWalk(BinaryTree node)
{
    if (node != null)
    {
        InOrderWalk(node.Left);
        nodes.Enqueue(node);
        InOrderWalk(node.Right);
    }
}

然后定义中序遍历的方法。这是一个递归算法。传入一个节点，如果不是null，就在其左孩子上调用同样的算法，直到找到“最左边”的节点，左子树遍历完后，将自己加入队列，然后对右边重复同样的操作。对于中序遍历，最左的孩子最先被发现，输出的时候也是最先输出，因此采用先进先出的队列。

public BinaryTreeEnumerator(BinaryTree<T> tree)
    {
        this.root = tree;
        currentNode = tree;
        nodes = new Queue<BinaryTree<T>>();
        InOrderWalk(tree);
    }
    public T Current { get { return currentNode.Value; } }
    object IEnumerator.Current { get { return Current; } }

    public void Dispose() { }
    public bool MoveNext()
    {
        if (nodes.Count != 0)
        {
            currentNode = nodes.Dequeue();
            return true;
        }
        return false;
    }

    public void Reset()
    {
        currentNode = root;
    }
}

接下来是构造函数和枚举器接口的实现。构造函数接受一个节点为参数，然后讲根节点和当前节点初始化为这个节点。然后初始化队列，并进行遍历保存顺序。 Current是一个只读属性，返回当前节点的数据，这样可以保证随时都是最新的数据。IEnumerator是范型版本的接口的基接口，我们直接间接调用一下范型宝贝的实现即可。Dispose我们直接留空，我们不需要特殊处理。 MoveNext负责前进枚举器。只要队列不为空，就表示遍历还没结束，我们从队列中拿出一个节点，然后把当前节点改成这个节点，返回true。如果队列为空，那么自然遍历已经结束，返回false。 Reset顾名思义重置枚举器，这里我们直接当前节点改为一开始的根节点，这就是我们定义root字段记录最初的位置的原因。最后我们让二叉树类实现IEnumerable<T>接口，完成。

public IEnumerator GetEnumerator()
{    
    return new BinaryTreeEnumerator(this); 
}
IEnumerator IEnumerable.GetEnumerator()
{    
    return GetEnumerator();
}

测试

最后我们构造上面图片中的二叉树，然后用foreach遍历。正确输出应当是：2，7，5，6，11，2，5，4，9。

static void Main(string[] args) 
{    
    var root = new BinaryTree(2, new BinaryTree(7), new BinaryTree(5));
    root.Left.Left = new BinaryTree(2);
    root.Left.Right = new BinaryTree(6, new BinaryTree(5), new BinaryTree(11));
    root.Right.Right = new BinaryTree(9, new BinaryTree(4));
    foreach (var node in root)
    {        
        System.Console.WriteLine(node);
    }
}