首先默认题中的“伪随机”一词指伪随机分布(Pseudo Random Distribution),“伪”的是分布而非随机产生的过程,与“真”随机分布(Uniform Random Distribution)相对。纠结于计算机受限于随机数生成器无法产生真随机的问题与本题无关。
最常用的伪随机是通过一个转换关系,将期望概率转换为一个初始概率值c和一个浮动概率值k,使得每次事件A的概率变为如下公式:
P(A) = c + k * n,其中n为自上次事件发生后连续未再发生的次数。
在这个公式下,每次随机事件不再是独立事件,而是与之前随机结果直接相关的事件,而显示给玩家的概率只是一个统计意义上的期望值,保证最终结果在样本足够大时与给定的期望概率一致。也就是说,运用这种伪随机分布来进行暴击等概率结算的游戏中,第一刀的暴击率是要比描述中的暴击率要低的,而随后如果连续很多刀没有暴击,接下来暴击的概率会大幅上升。而在n大到一定程度时,下次暴击的概率变成了大于1的值,从而必定暴击。
伪随机(Pseudo Random Distribution)与常规随机(Uniform Random Distribution)的概率分布如下(在P=25%时):
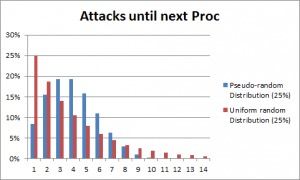
可以看出伪随机的特点在于分布更集中在一些区间。对暴击而言,更容易出现每x刀一次暴击的可能,也更难出现连续暴击。由于其分布可控性,在包括魔兽争霸3、Dota 2等知名游戏、以及一些国产开宝箱游戏中都有所应用。在这些游戏中,设计师用伪随机来避免一些极端情况的出现,尤其是在玩家群体足够大时,减少因这些极端情况而导致的负面影响。
那么这些极端情况到底有多极端呢?
让我们来找几个例子,以各类卡牌游戏中让人又爱又恨的开包为例吧。
假如某个游戏一次开包有1/30的概率(未做任何处理)出特别稀有的强力卡,并且多数玩家都是每天开一次包。从理想的角度来说,这个游戏希望能玩家每个月经历一次这样的喜悦,多了不珍惜,少了又坚持不下去。
现在这个游戏有1000万活跃玩家,那么在一个月内从未见到过任何强力卡的玩家约有362万(36.2%, 约等于1/e),三个月里这数值是47.3万(4.73%),坚持一年依旧从未见到强力卡的玩家平均也会有42个,而一年里完全没有这样的“非酋”玩家的概率几乎是零。
对于一个优质移动端卡牌游戏,这三个尺度分别对应了爆炸期、巅峰期、成熟期。前一个月有30%多的玩家从未经历过游戏的某部分核心乐趣,这部分玩家如果有一半都去社交圈或者论坛发个帖吐槽,会产生多少负面评价?这样的玩家能坚持多久,游戏又能活多久?
之前说了,这个游戏不希望通过提高概率来避免极端情况——这会导致其他玩家的获得概率也提升,那么这时候就得通过操控概率的手段来实现了。于是更好的做法应该是用上述的公式控制极端情况n的上限,比如设置到n的上限为45天。如果要吸引新入坑的玩家,让他们一开始能尝到甜头,还可以把每个玩家的初始P(A)设置到比较高的数值,在暴出强力卡以后再回归为正常的数值。
从某种意义上来说,伪随机控制下的随机因素在游戏中更难出现因运气因素而扭转局势的可能,更能提升游戏的竞技性。至于是否会使游戏变的更公平,要注意的是运气因素本身也是公平的,并不会影响每个玩家收益的期望。但我个人倾向于认为,使用伪随机在一定程度上能保证多数游戏的体验,虽然不影响公平性,但值得使用。而对于另一些把运气与戏剧性因素作为重要卖点的游戏而言,游戏玩法中的伪随机反而使游戏变得复杂臃肿,也因此变得不可取。
